How to Find the Center of a Circle

Today I wanted to share a quick geometry trick which you may find handy if you are working on a project that involves a circle shape: how to find the center of a circle.
The principle of it is based on the following theorem:
“A tangent always forms a right angle with the circle’s radius.”
Sounds pretty geeky right? I know… when the subject is math or computers I tend to get a bit geeky. But still I am not even close to Greg’s level when the subject is wine, music, or science (especially stuff related to outer space.) You may guess what fun parents we are 😀 … anyway, let’s get back to the tutorial.
Draw a line on a circle as shown below. Don’t worry about where the line is, because any line that crosses a circle is ultimately parallel to a tangent line. But the only important thing is that you draw your line to measure a simple number that is dividable by 2 as it will ease your job in next step.

Find the middle of that line and mark it. My line was exactly 8 inches, so I marked the middle at 4 inches.
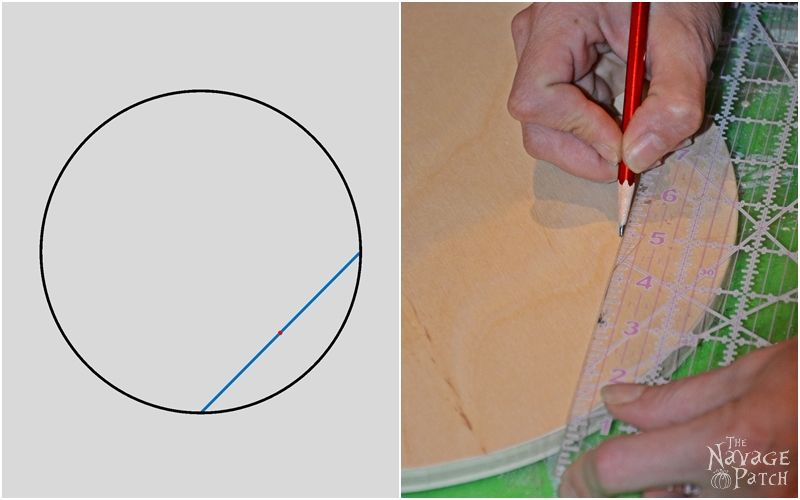
From that middle point, draw a right angle line long enough to pass what you deem the middle of the circle.

Now do the same steps once again on another side of the circle.


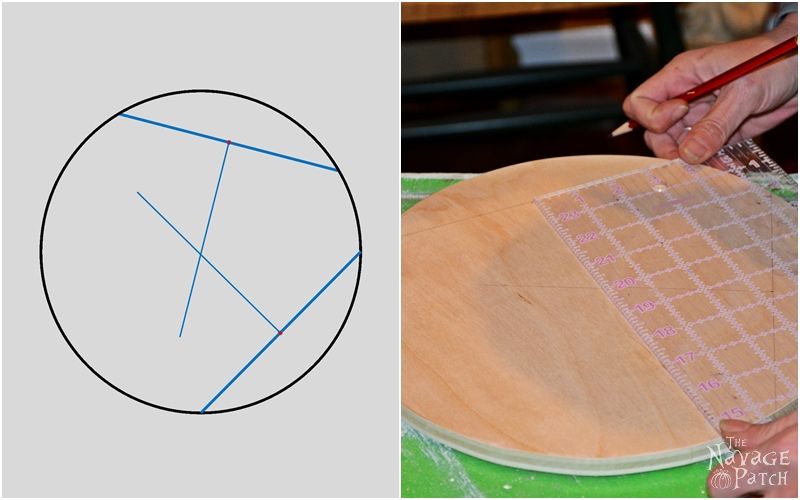
The point where your 2 right angle lines cross each other is the center of that circle.

It was pretty simple, right?
I hope you find this information useful when working on projects like tiered stands, clocks, round side tables, et cetera.
Handan, xo












Great information! Thank you.
Thank you so much, Teresa!
This is the easiest I have seen it explained. Thank you!!!
I am glad you think so… Thank you very much, Pam!
OH MY GOD I could KISS YOU FOR THIS!!!! The skill to do this has eluded me for years, and put the kill on a number of projects. Or I had just not to care whether I had the exact center or not, leading to some truly HILARIOUS results. I have SO bookmarked this. YOU ROCK.
Thank you so much, Theresa!
Thanks! I had already planned to trace a plate onto paper, cut out the circle and fold it in half and in half again. That might have worked, but your instructions would take a lot less time and be more accurate.
Thanks a bunch!
Thank you so much, Cathy! Your method is also very smart and could work excellent with circles which you can’t mark the surface with a pencil, such as glass. I’ll definitely keep your method in mind when I am working with glass circles. Thank you so much for sharing your method with me! 🙂
Yay, whoop, whoop a woman after my own heart. Geometry rocks and it just makes me more convinced that you and Greg are a match made in heaven. One of my all time favorites quotes by Pythagoras probably says it better than I ever could “There is geometry in the humming of the strings, there is music in the spacing of the spheres.”
Thank you so much, Michelle! That is indeed a beautiful quote from Pythagoras – I will have to use it in one of my crafting projects! And yes, Greg and I are a perfect match! 😉
Brilliant,, why didn’t l think of that, it was simple and easy to use when shown how to do it. It goes to show that at 78 yrs young your not to old to learn. Thanks